Pre-requirements:
Introduction:
প্রথমেই আশা করছি তোমরা উপরের pre-requirements শেষ করেছো। না করলে দয়া করে সেগুলো একটু দেখে নাও। তাহলে তোমাদেরই বুঝতে সুবিধা হবে। যাই হোক আমরা আগে ধাঁধাটি দেখে নেই। নিচের ছবিটি লক্ষ কর।
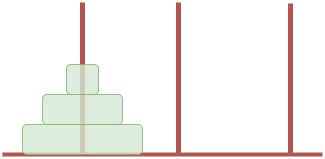
উপরের ছবির মতো তোমাকে তিনটা পিলার দেয়া আছে এবং প্রথম পিলারে ছবির মতো $n$ টা ডিস্ক দেয়া আছে, সাইজ অনুসারে সাজানো। এবার তোমার কাজ হলো প্রথম পিলারের ডিস্ক গুলোকে অন্য যেকোন একটা পিলারে নিতে হবে। শর্ত হলো শুধু কোনো পিলারের উপরের ডিস্কটা সরাতে পারবে আর একটা ছোট ডিস্কের উপর বড় ডিস্ক রাখতে পারবেনা। তোমাকে বলতে হবে এটি করা সম্ভব কিনা। আর যদি সম্ভব হয় তাহলে সর্বনিম্ন কতগুলো মুভ লাগবে সেটিও বলতে হবে। যদি বুঝে না থাকো তাহলে নিচের ছবি তিনটা দেখো।
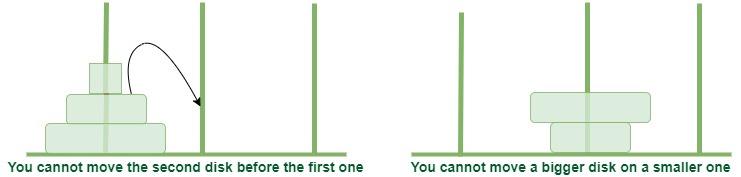
এখন আমরা এটি সমাধান করবো। এরকম সমস্যা সমাধান করার প্রথম ধাপ হলো ছোট মান নিয়ে একটু চেষ্টা করে দেখা। $n = 0$ হলে আমাদের 0 টা মুভ লাগবে। $n=1$ হলে আমাদের 1 টা মুভ লাগবে। $n = 2$ এর জন্য আমরা নিচের ছবিতে দেখাচ্ছি।
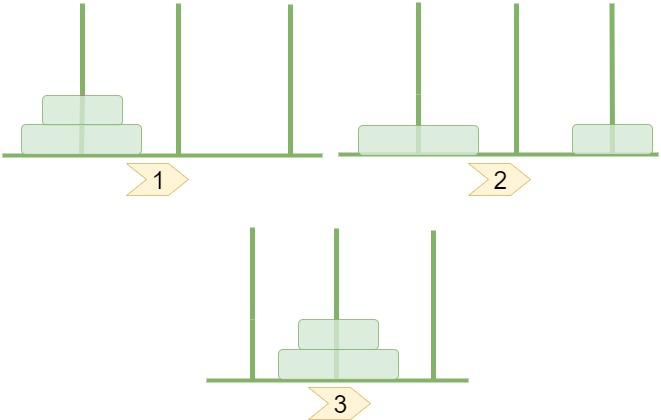
ওকে, দেখাই যাচ্ছে $n = 2$ এর জন্য আমাদের উত্তর আসছে 3। এবার 3 এর জন্য সিমুলেট করে দেখি।
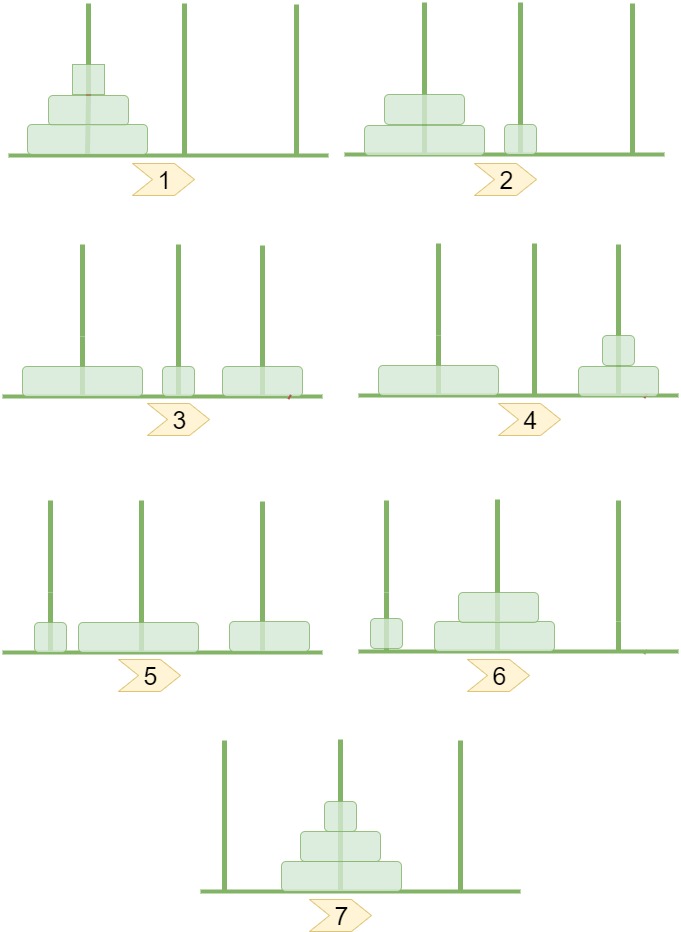
$n = 3$ এর জন্য উত্তর আসছে 7। এবার যারা বুদ্ধিমান তারা ঠিকই বুঝে ফেলেছ $n$ এর জন্য আমাদের উত্তর আসছে $2^n - 1$। এটা কিন্তু খুব সহজেই Induction দিয়ে প্রমান করে ফেলা যাবে। কিন্তু আমরা বুঝতে চাচ্ছি এখানে এটা কোথা থেকে এলো। হুট করে এখানে 2 এর পাওয়ার আসার কারন কি? চলো একটু চিন্তা করা যাক।
Why power of 2?
এখানে 2 এর পাওয়ার কেন কাজ করে সেটি জানার জন্য আমাদের বাইনারি নাম্বার নিয়ে একটু ঘাটাঘাটি করে দেখা লাগবে। তার আগে নাম্বার সিস্টেম নিয়ে একটু চিন্তা করে দেখি। আমরা নরমালি দশভিত্তিক যে নাম্বার সিস্টেম ব্যাবহার করি সেটির নাম্বার গুলো কেমন হয় আসলে? $0,1,2,3,4,5,6,7,8,9..$, এখানে দেখা যায় 9 এর পর আর কোন অংক বাকি নেই। তাই আমরা আমাদের সংখ্যাকে একপ্রকার left-shift করি। অর্থাৎ, একটা অংক ব্যাবহার না করে পুরো সংখ্যাকে একঘর বামে নিয়ে যাই এবং আবার শুরু থেকে শুরু করি। 9 এর পর 10, তারপর আবার এককের ঘরে আমরা আগের মতো $0,1,2,3….$ বসাতে থাকি। এভাবে আবার $99$ গেলে আবার আমাদের অংক ফুরিয়ে যায়, তখন আবার একঘর বামে নিয়ে আবার একইভাবে লিখতে থাকি। এবার বাইনারি নিয়ে চিন্তা করা যাক। বাইনারিতে মাত্র দুইটা অংক ব্যাবহার করা হয়, 0 আর 1। নিচে আমি 1 থেকে 8 পর্যন্ত সংখ্যাগুলোর বাইনারি দিচ্ছি। তারপর সেটি নিয়ে আমরা চিন্তা করে দেখব।
\[1 = 0001\\ 2 = 0010\\ 3 = 0011\\ 4 = 0100\\ 5 = 0101\\ 6 = 0110\\ 7 = 0111\\ 8 = 1000\\\]1 থেকে 2 তে যাওয়ার সময় চিন্তা করো। আমাদের সবথেকে ডানের ডিজিটটি 1। এর থেকে বড় ডিজিট আমরা নিতে পারবোনা। তাই আমরা পুরো ব্যাপারটাকে একটা left-shift করছি। করে 2 এর জন্য আমাদের বাইনারি আসলো $10$। এবার আবার আমরা $3$ এর জন্য ডান থেকে বিট পুরন করতে থাকবো। এবার চিন্তা করো, 1 থেকে 2 তে যাওয়ার পর যখন আমরা 3 নিয়ে কাজ করছি তখন কিন্তু আমাদের দুই নাম্বার বিটটা ফিক্সড। শুধু আমরা ডানদিক থেকে প্রথম ঘর নিয়ে কাজ করছি। 3 থেকে 4 এ যাওয়ার সময় একটা left-shift হচ্ছে এবং তারপর সেইম অবস্থা। সর্বডানের বিটটা অপরিবর্তিত রেখে আমরা শুধুমাত্র ডানপাশের বিটগুলোর জন্য কাজ করছি। অনেকটা রিকার্শনের গন্ধ পাওয়া যাচ্ছে, তাই না? নিচের ছবি দুইটা দেখো।

এখন ধরে নাও আমাদের একটা বিট নিয়ে নাড়াচাড়া করতে একটা করে মুভ লাগে। তাহলে চিন্তা করো, আমরা 7 বানানোর জন্য কি করছি? $7 = 0111$। তো, আমরা প্রথমে $3 = 0011$ বানাচ্ছি, তারপর এক মুভে একটা left-shift, তাতে এটা হয়ে যাবে $4 = 0100$। তারপর আবার একটা $3 = 0011$ বানাচ্ছি 4 এর বাম পাশের বিটটা ফিক্স করার পর। তাহলে আমরা যদি $n$ বানানোর মুভকে $f(n)$ নাম দেই, তাহলে দেখা যাবে $f(7) = f(3)+1+f(3) = 2f(3)+1$, আবার $f(3) = f(1)+1+f(1) = 2f(1)+1$। প্যাটার্নটা লক্ষ করেছো? এটা আপাতত সরিয়ে রাখি এবং আমাদের মূল সমস্যায় ফেরত যাই।
Main Problem:
মূল সমস্য়ায় আমরা এখন রিকার্সিভ একটা সলিউশন বের করবো। তারপর প্রমান করবো যে ওটাই সবথেকে অপটিমাল সলিউশন এবং তারপর প্রমান করবো ওটা থেকে কীভাবে $2^n-1$ আসলো এবং সেটি প্রমান করতে গিয়ে বাইনারি নাম্বার সিস্টেমের সাথে আমাদের এই সমস্যাটির সমাধানের সম্পর্কও বের করে ফেলব। আমরা আবার 3 এর জন্য সমাধান করার চেষ্টা করি। নিচের ছবিটি লক্ষ্য করো।
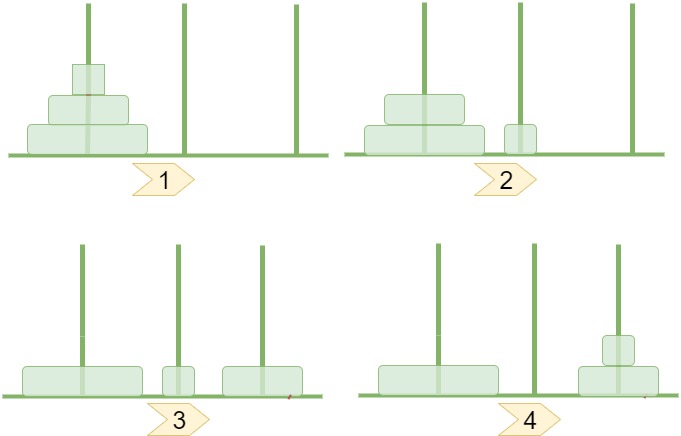
ছবিটি খুব মনযোগ দিয়ে দেখো। আমরা যদি 3 কে সরাতে চাই তাহলে আগে আমাদের প্রথম দুইটা ডিস্ক সরাতে হবেই, সরাতে বাধ্য। নাহলে আমরা 3 কে মুভ করাতে পারবোনা। আর 3 কে মুভ করাতে চাইলে বাকি সবগুলো ডিস্ককে একটা মাত্র পিলারেই থাকতে হবে। একাধিক পিলারে ডিস্কগুলো রাখলে 3 কে কিন্তু আমরা কোথাও রাখতে পারবোনা কারন এখন পর্যন্ত বের করা হয়েছে এরকম সব ডিস্কের সাইজই 3 এর থেকে কম। আর বাকি ডিস্ক গুলোকে যদি একটা পিলারেই রাখতে হয় তাহলে তাদের সর্ট করেই রাখতে হবে। নাহলে রাখা যাবেনা, কারন ছোটোর উপর বড় ডিস্ক রাখা যাবেনা। তাই উপরে যে পর্যন্ত করেছি, ওই পর্যন্ত ওটাই অপটিমাল।
এবার তাহলে কি হচ্ছে? আমাদের 3 কে বের করার জন্য শুরুতে উপরের দুইটাকে বের করে একটা পিলারে ফিক্স করতে হচ্ছে। তারপর আরেকটা খালি পিলারে 3 কে বসিয়ে তারপর আবার দুইটা ডিস্ককে 3 এর উপরে বসানো লাগছে। উপরের ছবির পর নিচের ঘটনাটি ঘটবে।
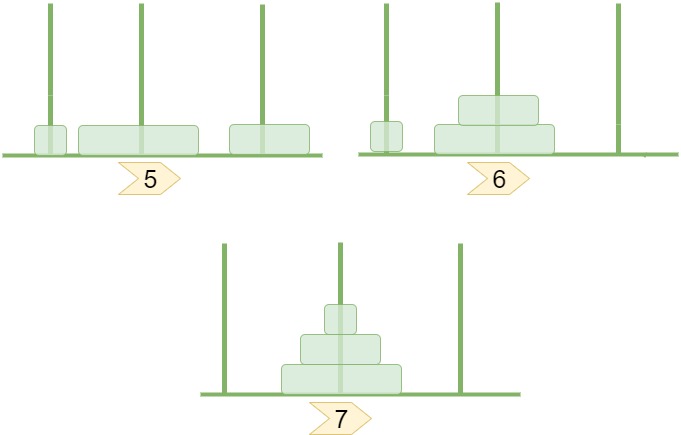
তাহলে $n$ টির জন্য মুভ যদি আমরা $g(n)$ ধরি তাহলে $g(n) = g(n-1)+1+g(n-1) = 2g(n-1)+1$। এবার আমাদের আগের বের করা ফর্মুলার কথা চিন্তা করো। ওখানে আমরা দেখেছিলাম $f(7) = f(3)+1+f(3) = 2f(3)+1$। এবার দেখো। আমরা 3 এর জন্য হাতে বের করেছিলাম, উত্তর হয়েছিল 7, তাহলে $g(3) = 7$ আর $g(2) = 3$। তাহলে $g(n) = g(n-1)+1+g(n-1)$ এ $n = 3$ বসালে হয়ে যাচ্ছে $f(g(3)) = f(g(3-1))+1+f(g(3-1))$ বা, $f(7) = f(3)+1+f(3)$। একদম কাটায় কাটায় সেইম জিনিস।
এখন এটা নাহয় বুঝলাম। কিন্তু তাও তো জিনিসটা ভিজুয়ালাইজ করতে সমস্যা হচ্ছে, তাই না? এখন তুমি এক কাজ করো। ডিস্কগুলোকে ডিস্ক মনে না করে একটা করে বিট মনে করো। একটা করে ডিস্ক সরানোর মানে তুমি একটা করে বিট পরিবর্তন করছো বলে ধরে নাও। যেমন 3 টা ডিস্ক নিয়ে কাজ করার সময় আগে 2 টা ডিস্ক সরাচ্ছো, তারপর 3 কে সরাচ্ছো, তারপর আবার দুইটা বিট নিয়ে কাজ করছো। ঠিক বাইনারি তে এটাই হয়। প্রথমে $3 = 011$ আছে ধরো। এটা বানাতে ধরো $k$ টা মুভ লাগে। এরপর আমরা এক মুভে একটা শিফট করছি, $4 = 100$। এরপর আবার ডানপাশের 0 দুইটার জন্য আবার $3$ বানাও। ঠিক এই জিনিসটাই কিন্তু হচ্ছে আমাদের টাওয়ার অফ হ্যানয়েও।
এবার আমরা এটা শিউর যে আমাদের রিকার্শন সঠিক। এবার রিকার্শন থেকে $2^n-1$ এর ফর্মুলা প্রমান করবো।
তাহলে আমরা এটা বীজগানিতিকভাবে প্রমান করে ফেললাম। চাইলে Induction দিয়ে প্রমান করা যেত। প্রথমে 0 আর 1 এর জন্য সূত্র বসিয়ে চেক করবে ঠিক আছে কিনা। তারপর $n$ এর জন্য $2^n-1$ সূত্রটিকে সত্য হিসেবে ধরে নিয়ে দেখবে সেটি $n+1$ এর জন্য সত্য মান দেয় কিনা। যদি দেয় তাহলেই আমাদের প্রমান সম্পন্ন হবে। ছোট করে আরেকটি কথা বলে রাখি। লুকাস বলেছিলেন যদি এই খেলাটি 64 টি সোনা দিয়ে বানানো ভারি ডিস্ক দিয়ে খেলা হয় তাহলে খেলা শেষ করতে করতে পৃথিবী ধ্বংস হয়ে যাবে। কারনটা স্বাভাবিক। একটা ডিস্ক সরাতে যদি 1 মিনিট করেও ধরি তাহলেও $2^{64}-1$ মিনিট লেগে যাবে। ততদিনে পৃথিবী ধ্বংস হয়ে যাওয়ার সম্ভাবনাই বেশি ![]() ।
।
আমি এই পোস্টে শুধু এটা কি এবং এটা কীভাবে কাজ করে সেটি বলেছি, আর এটির সাথে বাইনারি নাম্বারের সম্পর্ক দেখিয়েছি। পরে এটার টেকনিক ব্যাবহার করে আরো মজার কিছু সমস্যা সমাধান করার চেষ্টা করবো। আপাতত এই পর্যন্তই। হ্যাপি কোডিং।