আমরা সবাই জানি, মাঝে মাঝে অনেক দরকারে আমাদেরকে অ্যারে সর্ট করা লাগে, আর সবথেকে ভাল সর্টিং অ্যালগরিদম \(n\log { n }\) এ কাজ করে। কিন্তু আমরা তো \(O({ n }^{ 2 })\) এ সর্ট করতে পারি, কিন্তু জানি না, কিভাব \(n\log { n }\) এ সর্টিং করা যায়। যাই হোক, আজকে আমরা সেটাই জানার চেষ্টা করব।
Naive Approach
আমরা সবাই কিন্তু \(O({ n }^{ 2 })\) এ সহজেই সর্ট করতে পারি। এখন আমাদের উদ্দেশ্য হল একে \(n\log { n }\) এ রূপান্তর করা। দেখা যাক কি হয়।
আচ্ছা, আমাদের যদি ২ টা সর্টেড অ্যারে দেয়া হয়, আর যদি কোনোভাবে আমরা ২ টা অ্যারেকে \(merge\) করতে পারি, তাহলেই অনেক কাজ হয়ে যায়। কিন্তু আমি এখনি সেইদিকে যাচ্ছি না। ধরে নাও আমরা ২ টা সর্টেড অ্যারে \(O({ n })\) এ \(merge\) করতে পারি। আর তাই যদি পারি, তাহলে কি আমরা কোনভাবে ওই \(property\) ব্যাবহার করে সুবিধা পাব \(?\) দেখা যাক।
Better Approach 😮
ধরো একটা অ্যারে দেয়া আছে \(ara[12] = \left\{ 5,2,4,8,9,6,1,3,10,7,5,11 \right\}\) ।
তুমি করলে কি, এই অ্যারেকে ২ ভাগে ভাগ করে ফেললে।
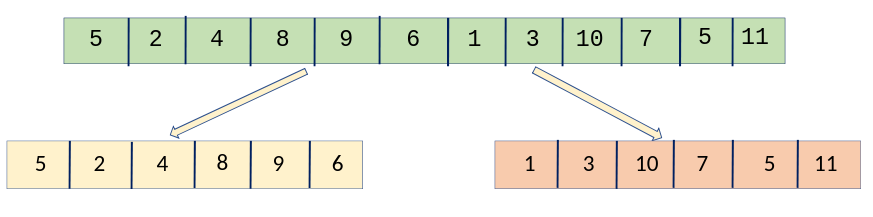
এখন চিন্তা করো, এভাবে ভাগ করে আমাদের লাভ কি \(?\) আগেই বলেছি আমাদের যদি ২ টা সর্টেড অ্যারে দেয়া হয়, তাহলে তাদেরকে \(merge\) করতে আমাদের \(O(n)\) সময় লাগে, কিভাবে \(?\) সেটা পরে বলছি, আগে ধরে নাও। আচ্ছা, হলো,এবার আমরা গাণিতিকভাবে দেখব, আমাদের কি উপকার হলো 🙂 আগে আসি, সম্পূর্ণ অ্যারে \(O({ n }^{ 2 })\) তে সর্ট করলে কি হতো।
\(⇒ O({ n }^{ 2 })\) \(⇒ O({ 12 }^{ 2 })\) ⇒ O(144)
এবার আমাদের নতুন Approach এর কি অবস্থা সেটা দেখা যাক 🙂
২ টা অ্যারে আছে, প্রথমটা সর্ট করতে লাগে \(O({ p}^{ 2 }) = 36\), দ্বিতীয় অ্যারে সর্ট করতে লাগে \(O({ q}^{ 2 }) = 36\) , বা , মোট \(72\) , আর \(merge\) করতে লাগবে \(O(n) = 12\) . সুতরাং মোট কাজ করতে হল \(72+12 = 84\). কোথায় \(144\), কোথায় \(84\) ! !😮 কি প্রো রে বাবা 😥 ।
এবার একটা \(twist\) দিচ্ছি। আমরা যদি প্রথম অ্যারেকে আবার \(2\) ভাগে ভাগ করি,তাহলে আমাদের প্রথম অ্যারে সর্ট করতে কত সময় লাগবে \(?\) অইত্ত, \(2\) ভাগ কে সর্ট করবা , তারপর \(merge\) করবা, হিসাব করে দেখ, মোট \(24\) টা অপারেশন করা লাগছে, আগে কিন্তু \(36\) টা করা লাগত। একিভাবে আমরা যদি ডান পাশের অ্যারেকেও \(2\) ভাগে ভাগ করে সর্ট করি, তাহলে আমাদের \(24\) টা অপারেশন করা লাগতেছে, তার মানে তখন সম্পূর্ণ অ্যারে সর্ট করতে আমাদের লাগবে হলো, \(24+24+12 = 60\) 😮 কোথায় \(84\) আর কোথায় \(60!\) আবার যেগুলাকে ভাগ করে \(2\) টা করে পেলাম, সেগুলাকে আরও ভাগ করে আরও কমানো সম্ভব না \(?\) এভাবে আমরা আসলে কতক্ষণ পর্যন্ত ভাঙতে পারব \(?\) চিন্তা করো তো দেখি \(?\) হুম, যদি কখনো ভাগ করতে করতে দেখো যে সাইজ \(1\) হয়ে গেছে, তাহলে কি আর ভাগ করা লাগবে ? লাগবে না তো, \(1\) সাইজের একটা অ্যারে তো আগে থেকেই সর্টেড! 😀 তাহলে আমরা \(recursion\) এর মতো করে চিন্তা করবো। ভাঙতে থাকব, যখন সাইজ \(1\) হয়ে যাবে, তখন আর সর্ট করা লাগবে না। এখন চিন্তা করো তো দেখি \(!\) যদি \(2\) পাশের অ্যারেই \(1\) সাইজের হয়, তাহলে আমাদের ওই অ্যারেগুলাকে কি নতুন করে সর্ট করা লাগতেছে? লাগতেছে না কিন্তু, শুধুমাত্র আমরা \(merge\) করে উপরের দিকে যেতে থাকব। তার মানে \(O({ n }^{ 2 })\) এ সর্ট করার যে বেপারটা, সেটা আমাদের করাই লাগতেসে না, শুধু \(merge\) করে করে আমরা উপরের দিকে উঠে যাচ্ছি, তাহলে আমাদের মোট merge করতে যা টাইম লাগবে, তাই হলো আমাদের \(Complexity\) 🙂 ।
merge Function 😮
এবার আসা যাক আমাদের সেই বিখ্যাত \(merge\) ফাংশনটার দিকে 😛

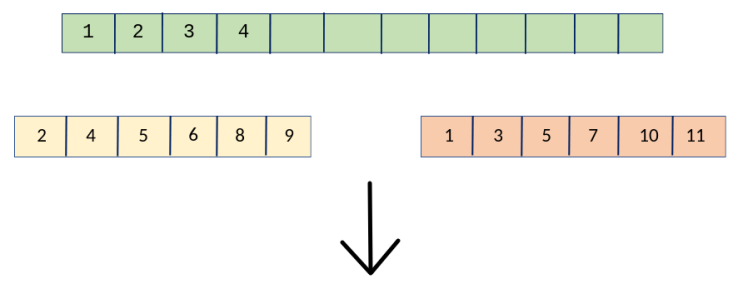
আমরা প্রথমেই উপরের ছবিদুটোর দিকে তাকাই । আমরা অ্যারে \(2\) টাকে সর্ট করেছি কোনোভাবে। এবার আমাদের \(merge\) করে বড়ো অ্যারে বানাতে হবে। যদি আমরা এই অ্যারে \(2\) টার মোট \(12\) টা সংখ্যাকে \(12\) টা অপারেশন করে সর্ট করতে পারি, তাহলেই আমরা ভালো করেই বুঝতে পারবো, জিনিষটা কিভাবে \(O({ n })\) এ কাজ করে। এবার নিচের ছবি দেখো। আমরা এই \(2\) টা অ্যারে থেকে \(1\) টা \(1\) টা করে এলিমেন্ট নিয়ে বড়ো অ্যারেটাতে বসাবো এবং ওই বড়ো অ্যারেটাতে ছোট \(2\) টা অ্যারের সবগুলো এলিমেন্ট সর্টেড অবস্থায় থাকবে। তার মানে আমরা \(2\)টা অ্যারেকে \(merge\) করে একটা বড়ো অ্যারে বানাচ্ছি, সেটাই হলো আমাদের মূল উদ্দেশ্য।
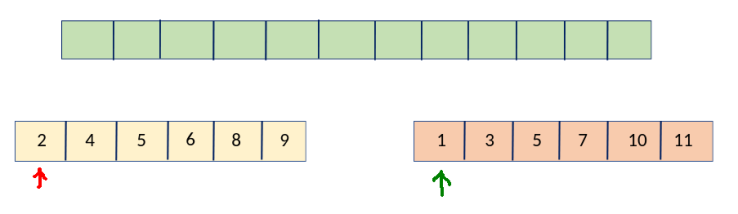
দেখতেই পারছো, আমরা নিচের ছোটো অ্যারে \(2\) টার প্রথম এলিমেন্টে একটা করে পয়েন্টার রাখি। এরপরের সবকিছু কহু সহজ, আমরা শুধু এই \(2\) টা পয়েন্টার দেখেই আমাদের সিদ্ধান্ত নিব। লাল আর সবুজ পয়েন্টারের মধ্যে যে এলিমেন্ট ছোটো,সেটি বড়ো অ্যারেতে ইনসার্ট করবো এবং সেই পয়েন্টার ডানদিকে একঘর সামনে নিব। যেহেতু, অ্যারে \(2\)টা সর্টেড, তাই আমাদের এই কাজটা করতে সমস্যা হবেনা। একটু চিন্তা করলেই বুঝতে পারবে জিনিসটা কেন কাজ করে। লাল আর সবুজ পয়েন্টারের আগের এলিমেন্টগুলা আগেই ইনসার্ট করা হয়ে গেছে , সুতরাং এভাবে নিলেই আমরা বড় অ্যারেটা সর্টেড আকারে পেয়ে যাবো। নিচের ছবিগুলা দেখ, একদম হাতে হাতে করে করে দেখিয়েছি, ছবিগুলো দেখলে মুল কনসেপ্ট বুঝতে কষ্ট হওয়ার কথা না 🙂
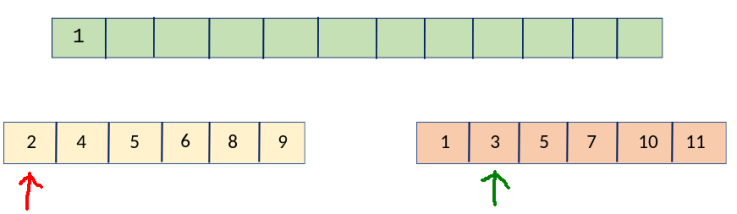
ডানপাশের অ্যারের পয়েন্টার \(1\) ঘর সামনে নিলাম, যেহেতু \(1 < 2\) । এভাবে নিচের ছবিগুলো পর্যবেক্ষণ কর 🙂।
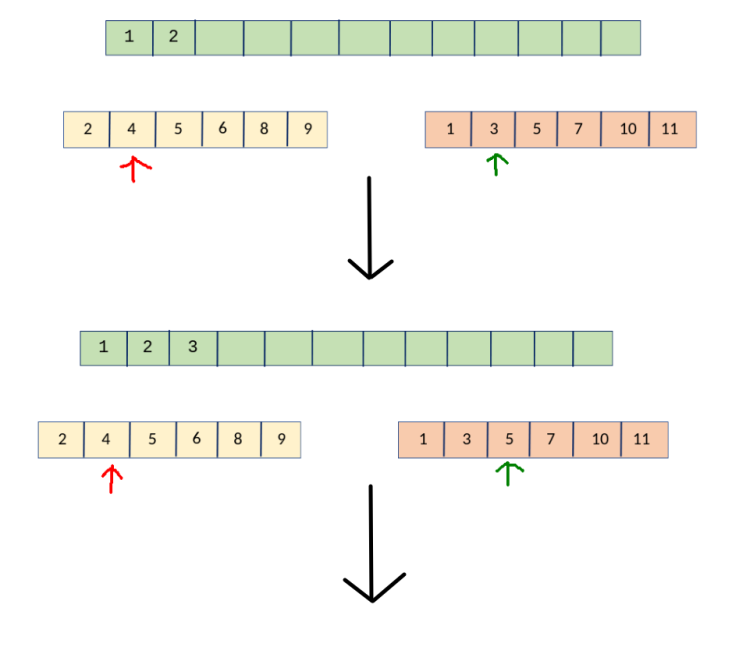
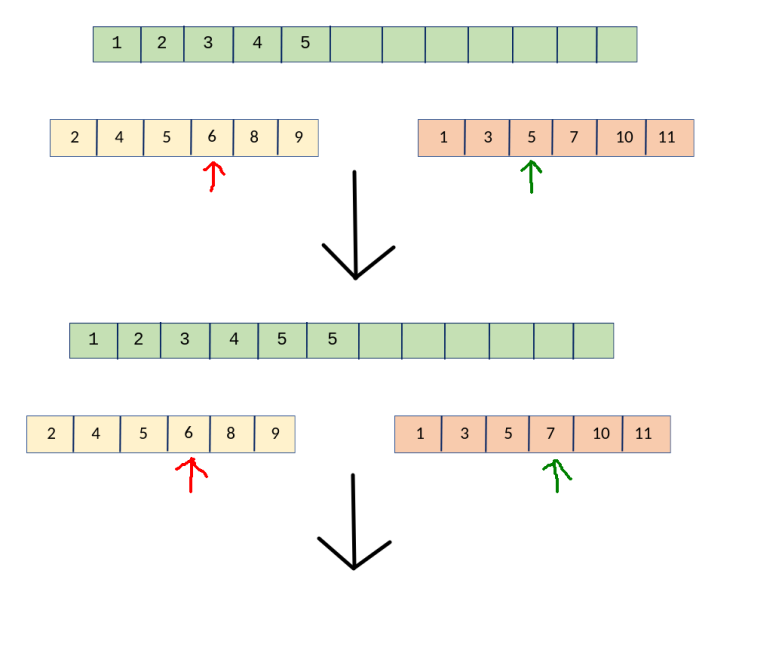
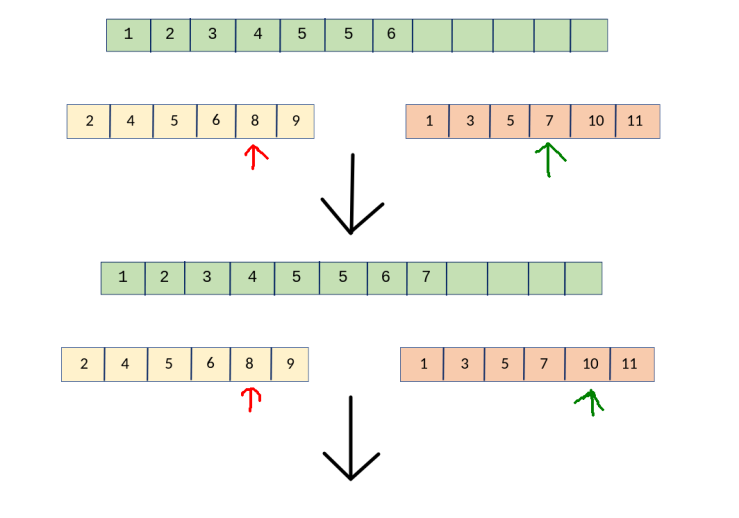
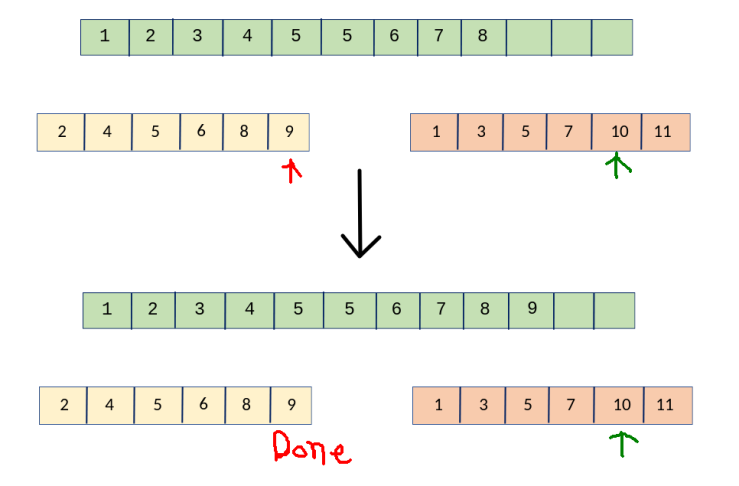
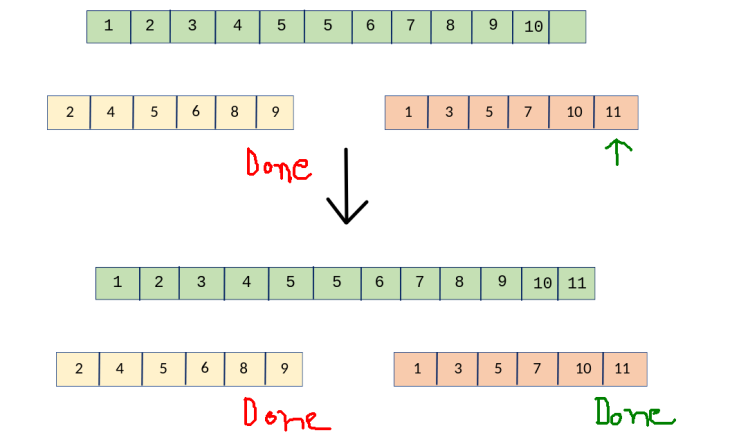
তাহলে, আমরা কি করছি আসলে \(?\) আমরা \(2\) টা পয়েন্টার নিচ্ছি, আর যেটা ছোটো, সেটাকে ওই বড় অ্যারেটার মধ্যে Insert করে, তারপর সেই পয়েন্টারকে এক ঘর সামনে নিচ্ছি, শেষ \(!\) আমরা সহজেই \(O({ n })\) এ \(merge\) করে ফেলতে পারছি 😀 । এবার কোডটা একটু দেখা যাক। আমরা একটা ফাংশন বানাবো, যেখানে আমরা \(2\) টা ছোটো অ্যারে আর একটা বড় অ্যারে দিব, আর তারা ছোট অ্যারে \(2\) টাকে \(merge\) করে বড় অ্যারেটাকে সর্টেড অবস্থায় আমাদেরকে দিবে , কি মজা \(!!!\)
void merge()
{
int i,j,k;
// here ara1[] = left array;
// here ara2[] = right array;
// here temp[] = the big array(where we are merging)
// here n means size of the left and right array
// here main_size means then size of the big array (mainly n*2)
//here i means pointer of left array
//here j means pointer of right array
for(i = 0,j = 0,k = 0;k <= main_size;){
if(i == n)temp[k] = ara2[j++];// it means we have inserted all the values of the left array
else if(j == n)temp[k] = ara1[i++];// it means we have inserted all the values of the left array
else if(ara1[i] < ara2[i])temp[k] = ara1[i++];// you know what it means :)
else temp[k] = ara2[j++];// you also know about it, think deeply :)
k++;//everytime we are increasing k, after inserting a value in the temp[] array
}
}
তো, কোড দেখে তোমরা বুঝে ফেলেছ যে কিভাবে \(merge\) করতে হয়। এবার একটা জিনিষ খেয়াল কর, আমরা আমাদের মুল যে টার্গেট, সেখানে \(2\) টা আলাদা অ্যারা কে \(merge\) করছি না, একটা অ্যারা এর \(2\) টা অংশকে \(merge\) করছি। তাহলে আমাদের কি আসলে \(2\) টা আলাদা আর্যা \(Declare\) করার দরকার আছে \(?\) একটু চিন্তা করে দেখ, আমরা যদি শুধু \(i\) অ্যার \(j\) পাঠাই তাহলেও কিন্তু আমাদের চলে যাচ্ছে। এখন চিন্তা কর দেখি, আমাদের সম্পূর্ণ সর্টিং ফাংশনটা কেমন হবে\(?\) আমরা কি করছি\(?\) অ্যারাটাকে প্রথমে \(2\) ভাগে ভাগ করতে থাকছি, অ্যার যখন ভাগ করা শেষ তখন \(merge\) করে উপরে উঠে যাচ্ছি। এই কাজটা কি তুমি একা একা করতে পারবে \(?\) \(30\) মিনিট চেষ্টা করে দেখ, তারপর নিচের কোডটা দেখ।
int num[1000];//main array
int temp[1000];//temp array
void mergesort(int low,int high)// sorts num[low....high]
{
if(low == high)return;//it is the basecase
int mid = (low+high)/2;
mergesort(low,mid);
mergesort(mid+1,high);
int i,j,k;
for(i = low,j = mid+1,k = low;k <= high;k++){
if(i == mid+1)temp[k] = num[j++];
else if(j == mid+1)temp[k] = num[i++];
else if(num[i] < num[j])temp[k] = num[i++];
else temp[k] = num[j++];
}
for(int i = low;i <= high;i++){
num[i] = temp[i];//inserting sorted list[low to high] from temp to main array..
}
}
আজ এ পর্যন্তই। \(merge\) \(Sort\) নিয়ে বকবকানি এখানেই শেষ। তুমি যদি সেগমেন্ট ট্রি পারো, তাহলে এই ব্লগটি পড়ে দেখতে পারো🙂 হ্যাপি কোডিং !