Pre-requirements:
- Binary numbers
- Basic Combinatorics
- Basic Recursion (If you want to understand tde codes)
- Induction (if you want to understand tde proofs)
Introduction:
তো আমরা আগে জেনে নেই জোসেফাস প্রব্লেমটা কি। এটা নিয়ে একটি গল্প আছে। একবার জোসেফাস আরও কিছু সৈন্য নিয়ে একটা গুহায় আটকা পড়লো। গুহা থেকে বের হলেই প্রতিপক্ষ আক্রমন করবে। তাই তারা চিন্তা করলো সবাই মিলে আত্যহত্যা করবে। কিন্তু জোসেফাসের ব্যাপারটি ভালো লাগলো না। যাই হোক, তারা প্রথমে গোল করে দাঁড়ালো এবং নিয়ম হলো, প্রথম জন তার পাশের জনকে মারবে। তার পরের জন আবার তার পাশের জনকে মারতে থাকবে। এভাবে চলতে থাকবে এবং শেষে একজন বেঁচে থাকবে। তো জোসেফাস এমনভাবে দাঁড়ালো যেন সেই সর্বশেষ ব্যাক্তি হয়। কারন তাহলে তাকে আর মরতে হচ্ছে না। আমরা এখন দেখবো জোসেফাস কীভাবে বের করেছিল যে কোথায় দাঁড়াতে হবে। যারা সমস্যাটি বুঝতে পারোনি তারা নিচের ছবি দেখ। তাহলেই বুঝতে পারবে আশা করি। ৮ জনের জন্য খেলাটি দেখানো হলো।
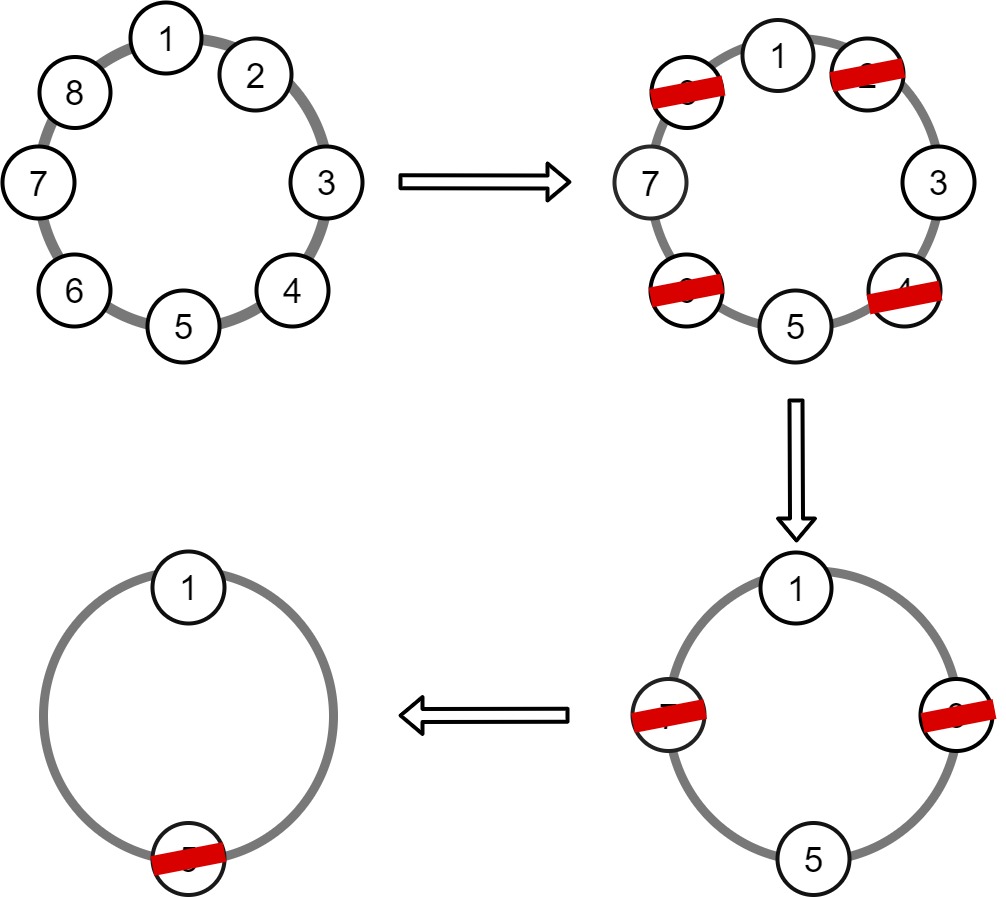
আশা করি প্রব্লেমটা বুঝতে পেরেছ। কীভাবে কাজটি করা হচ্ছে সেটি বুঝতে পারলে নিচে দেখতে পারো। আমরা এখন গাণিতিকভাবে বের করার চেষ্টা করবো সর্বশেষে কত নাম্বার লোক বেঁচে থাকবে।
Searching Pattern:
প্রথম ধাপে আমরা কিছু প্যাটার্ন বের করে সমস্যাটি সমাধান করার চেষ্টা করবো। তার আগে আমরা কিছু প্রেডিকশন করে নেই। যেমন, আমরা যে 8 টা নাম্বার নিয়ে ট্রাই করেছি, সেটির জন্য উত্তর এসেছে 1, তাহলে কি সবসময় 1 আসবে উত্তর? চলো দেখা যাক। আমরা একটু খাতায় করতে গেলেই বুঝবো 3 এর জন্যই দ্বিতীয় ধাপে 1 কাটা পরে। তাই সর্বদা উত্তর 1 হবেনা। আমরা আরেকটু সার্চ করে দেখি। 1 থেকে 16 পর্য়ন্ত প্রত্যেকটার জন্য শেষে কে থাকবে এটা খাতায় বের করে ফেল। আমি ধরে নিচ্ছি $n$ এর জন্য আমাদের উত্তর $f(n)$। এবার নিচের টেবিলটি দেখো(অবশ্যই ওটা নিজেরা খাতায় এঁকে বের করবে)।
| $n$ | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| $f(n)$ | 1 | 1 | 3 | 1 | 3 | 5 | 7 | 1 | 3 | 5 | 7 | 9 | 11 | 13 | 15 | 1 |
এখানে টেবিল দেখে আমরা একটা প্যাটার্ন দেখতে পাচ্ছি। প্রতি 2 এর পাওয়ার থেকে একটা সমান্তর ধারা $1, 3, 5…$ তৈরি হয়। এখন, আমরা যদি $n$ এর জন্য উত্তর বের করতে চাই, তাহলে আমরা এটা জানি। $n$ এর থেকে ছোট অথবা সমান 2 এর পাওয়ারের জন্য উত্তর 1, আর তারপর প্রতি একঘরের জন্য উত্তর দুই করে বারতে থাকে। অর্থাৎ, $n$ ছোট অথবা সমান সবথেকে বড় 2 এর পাওয়ার যদি হয় $2^k$ তাহলে আমাদের উত্তর হবে $2(n-2^k)+1$। এখন আমরা কিন্তু সমাধানটি পেয়ে গেছি বলে মনে হচ্ছে, কিন্তু আসলে সমাধানটি সম্পূর্ন হয়নি। কারন, আমরা 1 থেকে 16 পর্যন্ত একটা প্যাটার্ন সার্চ করে ফরমুলাটা দাঁড় করিয়েছি। কিন্তু এটা যে $n$ এর সকল মানের জন্য সঠিক উত্তর দিবে সেটি প্রমান করতে হবে।
Recursive Proof:
আমরা প্রমান করার আগে আরেকটা জিনিস প্রমান করবো। তারপর Induction ব্যাবহার করে আমাদের আগে করা প্যাটার্ন সার্চিং প্রমান করার চেষ্টা করবো। আমরা আগের মতোই আমাদের উত্তরকে $f(n)$ ধরে নিব। আমরা আগে $n = 10$ এর জন্য নিচের ছবিতে প্রথম ধাপ করবো এবং সেখান থেকে একটা সিদ্ধান্ত নিব। ছবিটা দেখ।
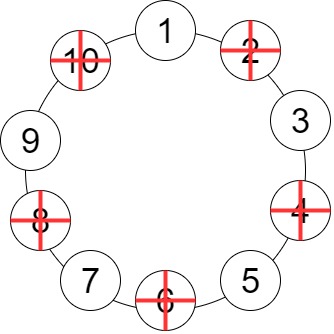
এখন দেখো, প্রথম ধাপ শেষ করার পর সকল জোড় সংখ্যা কাটা পরে যায় এবং শুধু বিজোড় সংখ্যাগুলো থেকে যাচ্ছে। আরও লক্ষনীয় বিষয় হলো একধাপে পূর্বের থেকে বর্তমান সংখ্যা অর্ধেক হয়ে গেছে। পূর্বে ছিল 10 টা, এখন একটা ধাপ শেষ করেই সংখ্যা 5 টা হয়ে গেছে। সংখ্যা 5 টা হয়ে গেছে এবং দেখা যাচ্ছে এখান থেকে রিকার্সিভ একটা আইডিয়া চলে এসেছে। একধাপের পর সংখ্যাগুলো হচ্ছে: $1,3,5,7,9$। এখন এই সংখ্যাগুলোই যদি $1,2,3,4,5$ হতো তাহলে আমাদের উত্তর হতো $f(5)$, তাই না? এবার একটা জিনিস লক্ষ্য করো, আমাদের একটা ইন্ডেক্সে কোন সংখ্যা আছে সেটা কিন্তু ততটা গুরুত্বপূর্ন না। কত নাম্বার ইন্ডেক্সের সংখ্যাটি শেষে বেঁচে থাকবে সেটাই মূল বিষয়। ওই ইন্ডেক্সে যে নাম্বার থাকবে সেটিই আমাদের উত্তর। নাম্বার না থেকে গরু ছাগল থাকলেও সমস্যা নেই। আর শুধু সেকারনেই দেখো একটা মজার জিনিস। আমরা $1,3,5,7,9$ সিকোয়েন্সকে $1,2,3,4,5$ দিয়ে ম্যাপ করতে পারি। যেখানে ম্যাপ করা লিস্টে একটা ভ্যালু $x$, আমাদের মেইন লিস্টে $2x-1$। তার মানে $1,2,3,4,5$ এর জন্য যে উত্তর হবে তার দ্বিগুনের থেকে 1 বিয়োগ করে দিলেই হয়ে যাবে। অর্থাৎ, $f(10) = 2f(5)-1$। এবং এটা n এর সকল জোড় সংখ্যার মানের জন্যই সত্য, যেহেতু প্রথম ধাপে শুধু জোড় সংখ্যা গুলো বাদ পরে যায়। তাই আমরা নিচের জিনিসটি লিখতে পারি।
\[f(2n) = 2f(n)-1 ~ ~ ~ ~ for ~ n \geq 1\]এবার বিজোড় সংখ্যার জন্য রিকারেন্স বের করি। আমরা বিজোড় সংখ্যাকে $2n+1$ আকাড়ে লিখতেই পারি। এবার নিচের ছবি দেখো, 9 এর জন্য প্রথম ধাপ কেমন হয়ে সেটা দেখিয়েছি।
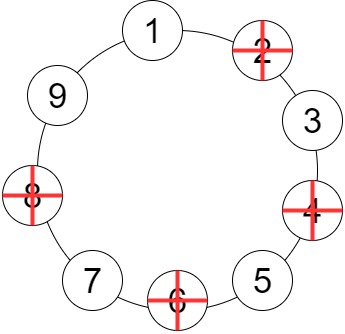
এখানে দেখো একটা জিনিস, $8$ কাটা যাওার পরেই 1 ও কাটা যাবে, যেটা ছবিতে দেখাইনি। তাই মূলত $1,2,3,4…9$ নিয়ে কাজ শুরু করে আমরা একধাপ পর $3,5,7,9$ পাচ্ছি। এখানেও দেখো, 4 টা নাম্বারকে ম্যাপিং করলে ম্যাপের $x$ হবে মূল সিকোয়েন্সের $2x+1$। তাহলে আমরা বলতে পারছি, $f(9) = 2f(4)+1$। আবার $9$ কে লেখা যায় $2 \times 4 + 1$। অর্থাৎ, আমরা আগের মতো নিচের জিনিসটি পেয়ে যাচ্ছি।
\[f(2n+1) = 2f(n)+1 ~ ~ ~ ~ for ~ n \geq 1\]আবার আমরা রিকার্শনের বেইস কেইস জানি, $f(1) = 1$। তাহলে সবগুলো জিনিস একত্রে লিখি:
\[f(2n) ~ ~ ~ ~ ~ ~ ~ = ~ 2f(n)-1 ~ ~ ~ ~ ~ ~ ~ ~ ~ for ~ n \geq 1\\ f(2n+1) = ~ 2f(n)+1 ~ ~ ~ ~ ~ ~ ~ ~ ~ for ~ n \geq 1\\ f(1) = 1\]Proof by Induction:
আমরা আগের প্যাটার্নটি নিয়ে আবার কাজ করবো এখন। যদি $n = 2^k+d$ হয় তাহলে আমাদের উত্তর হবে $2d+1$। এটা এখন আমরা প্রমান করবো। প্রমানের দুটি ধাপ আছে যদিও। একটা দেখাই, আরেকটা নিজেরা করবে।
Induction না বুঝলে একটু পড়ে নাও। আমি সংক্ষেপে বলছি। আমরা কোনো একটা জিনিস প্রমান করার জন্য প্রথম দেখবো সেটি বেইস কেইসে কাজ করে কিনা। করলে, আমরা ধরে নিব $n$ এর জন্য কথাটি সত্য। তারপর আমরা দেখব $n$ এর জন্য সত্য ধরে $n+1$ বা এরকম কিছুর জন্য প্রমান করবো, যাতে $n = 1,2,3…$ বসিয়ে আমরা অসীম পর্যন্ত সব সংখ্যার জন্য প্রমান করতে পারবো।
তো এখন তোমরা বেইস কেইসে দেখ আমাদের প্যাটার্নের সূত্র কাজ করে কিনা। কাজ করবে অবশ্যই। তারপর আমরা ধরে নিব $n$ এর জন্য বিষয়টি সঠিক। ওটাকে সঠিক ধরে যদি দেখি $2n$ এর জন্যও সঠিক আসে তাহলে আমাদের প্রমানের অর্ধেক সম্পন্ন হবে। এটা গেল বিজোড়ের জন্য প্রমান। আবার একইভাবে জোড়ের জন্য প্রমান করে দেখবো। একটা জিনিস খেয়াল করো, $2n = 2^k+l$ হলে $n = 2^{k-1}+\frac{l}{2}$ হবে। কেন হবে সেটি নিজেই চিন্তা করে দেখ। এবার মান বসাই।
\[f \bigg(2n \bigg) = 2f \bigg(n \bigg)-1\\ f \bigg(2^k+l \bigg) = 2f \bigg(2^{k-1}+\frac{l}{2} \bigg)\\ f \bigg(2^k+1 \bigg) = 2 \bigg(2 \frac{l}{2} \bigg)-1\\ f \bigg(2n \bigg) = 2l-1\\\]দেখো, আমরা $f(n)$ এর মান সত্য ধরে সেটির মান বসিয়ে দেখতে পাচ্ছি $f(2n)$ এর জন্যও জিনিসটি সত্যি। এবার $f(2n+1)$ এর জন্য নিজে চেষ্টা করো। প্রমান করা একদম সহজ। আর এটা করতে পারলেই আমাদের প্রমাণ সম্পন্ন হবে।
Visualizing Binary Representation:
এতোক্ষনে আমরা জোসেফাস সমস্যাটি সমাধান করে ফেলেছি। ওটার রিকার্সিভ প্রমান দেখেছি, সেটা থেকে আমাদের প্যাটার্নের প্রমান করেছি। এবার আমরা $n$ এর বাইনারি নাম্বার নিয়ে একটু কাজ কারবার করবো। দেখা যাক ভালো কিছু বের হয় কিনা।
আমরা একটু আগে দেখেছি, প্রতি একবার কাটাকাটি করলে লোকের সংখ্যা অর্ধেক হয়ে যায়। তাই এখানে 2 এর পাওয়ারের একটা ব্যাপার তো আছেই অবশ্যই। আর সেখান থেকেই বাইনারি নিয়ে চিন্তা করাটা জরুরি।
ধরি একটা সংখ্যা $n = b_{m}b_{m-1}b_{m-2}….b_{3}b_{2}b_{1}$। এখানে $b_i$ মানে $n$ এর i তম বিট। আমরা ধরে নিচ্ছি $n$ এর বাম পাশে কোনো লিডিং 0 নেই। কারন শুরুতে $0$ রাখার কোন মানে হয়না। তাহলে $b_m$ সর্বদা 1 হবে। তাহলে আমরা $n = 1b_{m-1}b_{m-2}….b_{3}b_{2}b_{1}$ ধরতে পারি। এবার আমরা আমাদের সূত্র থেকে জিনিসপত্র বের করার চেষ্টা করবো। আমরা সবথেকে বড় $k$ বের করেছিলাম যেন $2^k \leq n$ হয়। তারপর সেটা $n$ থেকে বাদ দিয়েছি, $l = n-2^k$ এবং তারপর আমার উত্তর হয়েছে $2l+1$। এবার এখানে বাইনারিতে কি ঘটছে সেটা দেখা যাক।
সর্বশেষ লাইনে কি লিখেছি সেটা আরেকবার খেয়াল করো আর একটু চিন্তা করে দেখ। ওপরের ব্যাপারটি থেকে স্পষ্টতই দেখা যাচ্ছে $n$ এর উপর একবার জোসেফাস চালালে শুধু $n$ এর বাইনারির শেষ বিটটি শুরুতে চলে আসে। বাকি সব ঠিকঠাক থাকে। এটাই উত্তর :o এখন আমরা যদি বারবার জোসেফাস চালাতে থাকি, তাহলে একটা সময় এরকম হয়ে যাবে যে $f(n) = n$। আর তখন আমরা যতবারই জোসেফাস চালাই, উত্তর শুধু $n$ ই আসতে থাকবে। এটা কখন হবে এবং কেন হবে? এটা বের করতে চাইলে তোমাদের একটু চিন্তা করতে হবে। এটি তোমাদের উপর ছেড়ে দিচ্ছি। SCB-PA Inter School and College Programming Contest 2019 এ এটি দিয়ে একটা সমস্যা এসেছিল। আমি যে সমস্যাটি তোমাদের সমাধান করতে দিলাম সেটি তোমরা সমাধান করতে পারলে ওই iscpc এর সমস্যাটিতেও 100 তুলতে পারবে।
আজকে এই পর্যন্তই। সবাইকে ধন্যবাদ। happy coding।