Programming Throwdown

Pre-requirments:

• Disjoint Set Union Finding

• Basic Graph Theory

• Basic Complexity Analysis

Introduction:

আমি আশা করছি তোমরা উপরের Pre-requirements মোটামুটি বুঝে পড়ে ফেলেছ। না পড়ে থাকলে আগে ওটা দেখে নাও। যাই হোক, DSU এর মূল ব্যাপার হলো এটার complexity। যদি আমরা শুধু rank compression করি তাহলে $m$ বার অপারেশন চালালে মোটামুটি complexity হবে $O( m \log{n})$। কিন্তু যদি আমরা Rank compression আর path compression দুটোই করি তাহলে complexity দাঁড়াবে $O(m \ \alpha (n)) \approx O(m)$। এখন কথা হলো, এটা কোথা থেকে আসলো? এরকম complexity হুট করে চলে আসার কারন কি? জানতে হলে এই কথাটি দেখে নাও।

ওকে, এখন মজা করা বাদ দিয়ে আমরা ব্যাপারটা প্রমান করে দেখব। আমরা প্রথমে Rank Compression এ কেন complexity $O(\log{n})$ হয় সেটা দেখবো। তারপর দেখবো কেন Path Compression + Rank Compression করলে complexity দাঁড়াবে $O(m \ \alpha (n)) \approx O(m)$।

Rank Compression

আমরা Rank Compression এর জন্য সবথেকে অপটিমাল এজ লাগিয়ে ট্রি এর height যতটুকু সম্ভব বড় করার চেষ্টা করবো। এবং Proof by contradiction এর মাধ্যমে প্রমান করবো যে ট্রি এর হাইট $O(\log{n})$ এর বেশি হবেনা।

আগে এক কথায় জেনে নেই Rank Compression আসলে কি জিনিস। মূলত আমরা যে দুইটা নোডের ইউনিয়ন করি, তখন যে নোডের কম্পোনেন্টের সাইজ বেশি সেটিকে প্যারেন্ট বানাই আর আরেকটাকে চাইল্ড বানাই। ‍if(size[u] > size[v])Union(u,v);else Union(v,u) অনেকটা এরকম।

আমরা শুরুতে নিচের ছবিটি লক্ষ্য করি। এটি হলো প্রথম ধাপ, যেখানে প্রত্যেকটা নোডের প্যারেন্ট সে নিজেই।

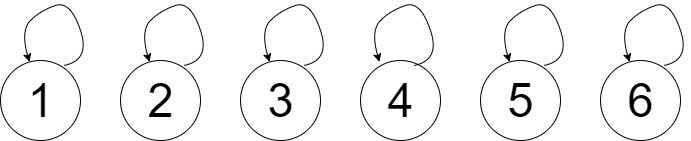
এবার আমরা নোডগুলোর ইউনিয়ন করতে থাকবো এবং এমন ভাবে ইউনিয়ন করবো যাতে ট্রি এর হাইট যতটুকু সম্ভব বাড়ানো যায়। আমরা নিচের ছবিতে 1 আর 2 নাম্বার নোড যুক্ত করেছি এবং সেটির প্যারেন্ট 1।

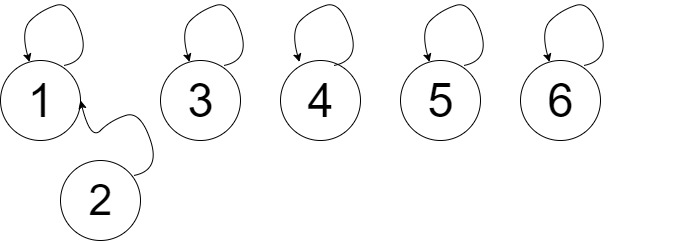
এবার ট্রিতে পাঁচটি কম্পোনেন্ট আছে। প্রথম কম্পোনেন্টের সাইজ 2, বাকিগুলোর 1। এখন আমরা যদি তিন নাম্বার নোডকে প্রথম কম্পোনেন্টে অ্যাড করি, তাহলে প্রথম কম্পোনেন্টের সাইজ হয়ে যাবে 3, কিন্তু হাইট কিন্তু 1 ই থাকবে। বিশ্বাস হচ্ছে না? তাহলে নিচের ছবিটি দেখো।

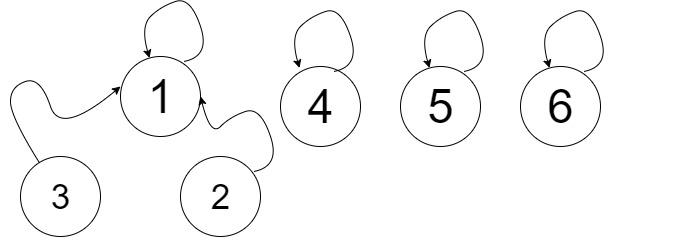
আমরা যদি উপরের ছবির মতো বারবার প্রথম কম্পোনেন্টে নোড ইউনিয়ন করতে থাকি তাহলে সর্বদাই আমাদের ট্রি এর হাইট একের থেকে বাড়ানো সম্ভব না। তাই প্রথম কম্পোনেন্টে নোড বসানো অপটিমাল না। সবথেকে অপটিমাল হয় আমরা যদি ছোট ছোট ট্রি বানিয়ে সেটা মার্জ করি। তাই আমরা আগে দুইটা দুইটা করে নোড একসাথে করে তিনটা কম্পোনেন্ট বানাবো। নিচের ছবি দেখ।

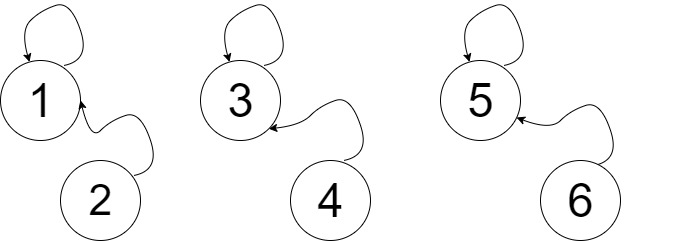
এখনও কিন্তু আমাদের কাছে তিনটা কম্পোনেন্ট আছে এবং ট্রি এর হাইট 1। কিন্তু এখন আমরা একটা একটা করে ট্রি এর হাইট বাড়াতে পারবো। 3 আর 1 কে ইউনিয়ন করে দেই। যেহেতু আমরা পাথ কম্প্রেস করছি না, তাই অনেকটা নিচের ছবির মতো একটা ঘটনা ঘটবে।

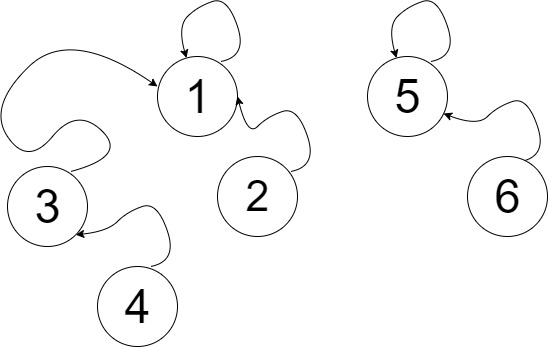
অর্থাৎ, আমরা এখন একের বেশি দৈর্ঘ্যের পাথ পাচ্ছি ট্রি তে - [1 --> 3 --> 4] , দুই সাইজের। এবার 4 আর 5 কে ইউনিয়ন করি। যেহেতু পাথ কম্প্রেশন করছি না, তাই শুধুমাত্র 5 প্যারেন্টের সাথে 4 এর প্যারেন্টের ইউনিয়ন হবে। 5 এর প্যারেন্ট 5 নিজেই এবং 4 এর প্যারেন্ট 3, তাই 5 এবং 3 এর ইউনিয়ন হবে। নিচের ছবিটি দেখো।

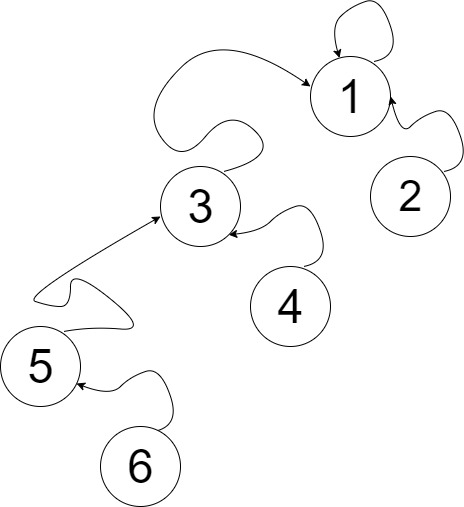
এখন এখানে কিন্তু আমরা একটা 3 height এর একটা পাথ পেয়ে যাচ্ছি [1-->3-->5-->6]। কিন্তু অন্যভাবে সাজিয়ে কি এর থেকে বেশি পাওয়া সম্ভব? উত্তর হচ্ছে না, কারন আমরা যতবার সমান সমান সাইজের দুইটা নোডকে মার্জ করবো আমাদের লাভ তত বেশি। কারন একটার সাইজ বড় হয়ে গেলেই ট্রি এর পাথ কমে যাচ্ছে। তাই এর থেকে ভালো সমাধান পাওয়া যাবেনা। এখন, 6 টা নোডের জন্য আমরা ট্রি এর হাইট দেখতে পাচ্ছি 3, তো কোন কিছু বোঝা যাচ্ছে কি? আসলে ট্রি এর অপটিমাল দৈর্ঘ্য হবে $\left \lceil {log_2{n}} \right \rceil$।

এটা অবশ্যই আমরা ফিল করার চেষ্টা করবো। আমরা দেখতে পেয়েছি উপরে, আমরা যদি ইউনিয়ন করার সময় কম্পোনেন্ট সাইজগুলো ব্যালেন্স করতে পারি তাহলে সেটি আমাদের জন্য অপটিমাল সলিউশন দিবে। আমরা একপাশে নোড বেশি দিতে গেলেই আমাদের জন্য ট্রি এর হাইট আরো কমে যাবে বাড়ার পরিবর্তে। তাই আমাদের যদি $n$ টা নোড থাকে ($1, 2, 3…….n$), তাহলে অপটিমাল ধরলে প্রথম ধাপে সব কম্পোনেন্টের সাইজ 1, তার পরের ধাপে সবগুলোর সাইজ 2 হবে এবং অর্ধেক কম্পোনেন্ট কমে যাবে। তার পরের ধাপে মূলত সবগুলোর সাইজ হয়ে যাবে 4 এবং ধাপ 2 থেকে কম্পোনেন্ট সাইজ আবার অর্ধেক হয়ে যাবে। এভাবে কম্পোনেন্টগুলোর সাইজ প্রত্যেক ধাপে দ্বিগুন হচ্ছে এবং কম্পোনেন্টের সংখ্যা অর্ধেক হয়ে যাচ্ছে। আর এর জন্যই আমরা ট্রি এর হাইট পাচ্ছি $(\log{n})$। আর যদি অপটিমালি আগাতে না চাই তাহলে অবস্থা আরো খারাপ হবে এবং আমাদের ট্রি এর হাইট আরো কমে যাবে।

আশা করি তোমরা DSU তে Rank Compression এ কেন ট্রি এর ম্যাক্স হাইট $\log{n}$ হয় সেটি ফিল করতে পেরেছো। পরবর্তী ব্লগে আমি Path Compression নিয়ে কথা বলবো। তার পরের ব্লগে DSU দিয়ে করা যায় এরকম কিছু কুল এবং দরকারি ট্রিক্স নিয়ে আলোচনা করবো। হ্যাপি কোডিং।

একই ক্যাটাগরির নিচের পোস্ট(গুলি) পড়ে দেখতে পারো:

1. SQRT Tree
2. Offline Query Solution Trick
3. Disjoint Set Union (Rank + Path Compression)
4. Merge Sort Tree (MST)

একই Difficulty এর বাকি পোস্টগুলোর লিস্ট দিয়ে দিচ্ছি, পড়ে দেখতে পারো:

1. Convex Hull
2. Basic Dynamic Programming(Part 1)