Pre-requirements:
Introduction:
আমি আশা করছি উপরের Pre-requirements কম্প্লিট করে ফেলেছ। এবার আমরা একটু জেনে নেই পাথ কম্প্রেশন কি। তার আগে একটু মনে করে নেই Rank Compression কি ছিল। মূলত আমরা Union করার সময় যে ট্রি এর সাইজ বড় সেটির প্যারেন্টকে মূল প্যারেন্ট বানাচ্ছিলাম। আর সেটির জন্য আমাদের ট্রি এর ম্যাক্সিমাম height ছিল $O( \log{n})$। তাই m বার অপারেশন চালালে complexity হয় $O(m \log{n})$। এখন, পাথ কম্প্রেশন হলো, আমরা যখন নিচ থেকে উপরে যাবো রিকার্শন করে, তখন আমরা প্যারেন্ট আপডেট করতে থাকবো। অর্থাৎ, অনেকটা নিচের মতো করবো।
void Find(int u){
if(u == parent[u])return u;
return parent[u] = Find(parent[u]);// this is the path compression
}
কোডটা না বুঝে থাকলে আগে Pre-requirement পড়ে শেষ করো। শাফায়েত স্যারের ব্লগে এটি কীভাবে করা হয় এবং কোডটি কীভাবে কাজ করে সেটি বলা আছে। তবে এটির Complexity কীভাবে আসলো সেটি বলা নেই। আজকে আমি সেটাই চিন্তা করে বের করবো। রিকার্শনটা কীভাবে কাজ করে সেটা বুঝতে পারলে নিচে পড়তে থাকো।
আমরা Path Compression এর ক্ষেত্রে কয়েকটা জিনিস একটু ধরে নিব বোঝার সুবিধার্থে। ধরো আমরা $n$ টি নোড নিয়ে কাজ করছি এবং আমরা $m$ টা অপারেশন চালাবো। এবার আমরা এটাও ধরে নিচ্ছি সবগুলো নোডকে Rank Compression ব্যাবহার করে Union করা হয়েছে। নিচের ছবি দেখো, ধরো বাম পাশের ছবিটি আমাদের Rank Compression করা ট্রি, আর ডানের টা নোড 5 এ Path Compression চালানোর পরের অবস্থা। আমরা নোড 5 কে যখন কম্প্রেস করেছি, তখন সে রিকার্সিভলি তার প্যারেন্টে গিয়েছে, এবং সেটি আবার তার প্যারেন্টে গিয়েছে, এভাবে 1 পর্যন্ত যাওয়ার পর প্রত্যেকের প্যারেন্ট সরাসরি 1 হয়ে যাচ্ছে। অর্থাৎ, 5 এর যতগুলো প্যারেন্ট আছে, এই একটা অপারেশনের পর সবগুলোর সাথে 1 এর দুরত্ব মাত্র 1।
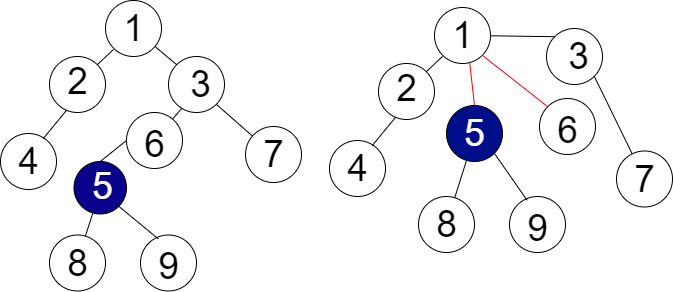
দূরত্ব 1 হওয়ার কারনে পর্বর্তীতে আমরা ওদের কোনো একটায় কুয়েরি করলে সেটার জন্য উত্তর $O(1)$ এই পেয়ে যাবো।
এখন একটা জিনিস চিন্তা করো দেখো। আমরা কি করছি? আমরা একটা নোডে পাথ কম্প্রেস চালালে ওই নোডের উপরে যারা আছে সবগুলোই অপটিমাইজ হয়ে যাচ্ছে, যার মানে সবগুলোর সাথেই মূল প্যারেন্টের ডিসটেন্স 1 হয়ে যাচ্ছে। আর আমরা যখন কোনো নোডের মধ্যে পাথ কম্প্রেস চালাচ্ছি, তখন সে উপরে উঠছেও ওই পরিমানই। যার মানে, আমি যদি একটা নোড x এ পাথ কম্প্রেস চালাই এবং তার উপরে y টা নোড থাকে তাহলে সে উপরে উঠবে y বার এবং সবগুলো নোড 1 এর সাথে সরাসরি যুক্ত হয়ে যাবে। তাই, অভারঅল মোটামুটি $\sim O(1)$ পার নোডেই কিন্তু কম্প্রেস হয়ে যাচ্ছে। তাই যদি হয় তাহলে কিন্তু আলটিমেটলি আমরা $m$ টা অপারেশন চালালে আমাদের টোটাল Time Complexity হবে $\sim O(m)$। যদিও সরাসরি m টা অপারেশন হবেনা, তবে মোটামুটি $4m$ এর বেশি যাবেনা। এটাও প্রমান করা যায় তবে আপাতত প্রমান করাটা জরুরি না, কারন আমার মনে হয় আমরা জিনিসটা ফিল করতে পেরেছি।
এখন কথা হলো, আমি কেন ব্যাপারটা গানিতিকভাবে ব্যাখ্যা করলাম না? কারন এটার গানিতিক প্রমান বেশ কঠিন। আমি উপরে যেভাবে ব্যাখ্যা করলাম, এটা কিন্তু গানিতিক প্রমান না। আমরা যেটা করেছি সেটাকে Intuition বলা যায়। জাস্ট আমরা একটা অবজারভেশনের মাধ্যমে ফিল করতে পারছি যে Path Compression এর Complexity $O(m)$ এর কাছাকাছি। আমাদের জন্য আপাতত এটুকুই যথেষ্ট। কিন্তু আমরা কিন্তু জিনিসটি প্রমান করিনি। আমরা 100% শিউরিটি দিয়ে বলতেও পারবোনা যে কতগুলো অপারেশন লাগবে। আমরা জাস্ট একটা আইডিয়া পেয়েছি যেটা ব্যাবহার করে আমরা মোটামুটি একটা Intuition দাঁড় করানো যায়। যাই হোক, এটার গাণিতিক প্রমান না করার মূলত দুইটা কারন ছিল আমার। প্রথমত এটা বেশ কঠিন এবং এর ডিপেন্ডেন্সি অনেক বেশি। যার মানে ওটা ব্যাখ্যা করার জন্য আরও শত শত জিনিস নিয়ে আগে কথা বলতে হবে। Discrete Mathematics, Complexity analysis নিয়ে একদম গঠনমূলক বিশ্লেষনের ক্ষমতা থাকতে হয়। ওগুলোর জন্য অনেক কিছুই আগে থেকে জানা থাকতে হয়। দ্বিতীয় কারন হলো, এইযে ডিপেন্ডেন্সির কথা বললাম, এগুলো আমার নিজেরই শেষ করা হয়নি। আমি গতকাল রাতে এই Path Compression এর গানিতিক প্রমান পড়তে গিয়ে দেখলাম, ওখানে যে গানিতিক নোটেশন গুলো ব্যাবহার করা হয়েছে আমি সেগুলোর মানেই জানি না। যদিও ওগুলোর ডেফিনিশন গুলোর রেফারেন্স দেয়া আছে, আমি সেই রেফারেন্সে গিয়ে দেখি ওগুলোর জন্যও আবার আরো অনেক কিছুর ডেফিনিশন-প্রমান জানতে হয়। তাই আমার মনে হয় ওটা নিয়ে পড়াশুনা করা অনেক সময়-সাপেক্ষ ব্যাপার। তাই ওটা নিয়ে সময় নিয়ে লিখতে হবে। পরবর্তী সময়ে এটা নিয়ে পড়াশুনা করে তারপর গানিতিক প্রমান নিয়ে লিখব চিন্তা করেছি। আর যারা প্রমানটা পড়তে চাও তারা Introduction to Algorithms 3rd Edition Page 573 তে গেলেই প্রমানটি খুঁজে পাবে।
আজকে এই পর্যন্তই, হ্যাপি কোডিং।